Sistem Getaran Pegas

Salah satu contoh getaran harmonis yang paling sering dikaji adalah gerak benda yang digantung dalam pegas. Selalu ada anggapan sederhana bahwa massa pegas diabaikan dan pegas tidak dalam keadaan mulur atau mengalami pertambahan panjang secara terus menerus. Selain itu sisi gaya non konservatif seperti gesekan juga diabaikan. Fokus pembahasan utama pada bagian ini tentunya akan lebih menekankan pada faktor apa saja yang mempengaruhi frekeunsi sistem pegas. Sistem pegas terdiri dari pegas yang kemudian digantungi beban. Pada keadaan ini, pegas akan mulur mencapai panjang akhir tertentu. Pertambahan panjang pegas dalam keadaan ini digunakan untuk menghitung konstanta gaya pegas. Simaklah gambar di bawah ini.

Pada keadaan setimbang seperti gambar di atas, gaya berat yang bekerja pada benda akan diimbangi oleh gaya pegas ke atas. Ketika pertambahan panjang yang terjadi adalah delta y, konstanta pegas dapat dihitung sebagai berikut:

Perlu diketahui bahwa gaya pegas (pemulih) dipengaruhi oleh pertambahan panjang pegas dan arahnya selalu melawan arah simpangan. Ketika benda yang digantung tersebut ditarik lagi sampai simpangan tertentu dan dilepaskan, benda akan mengalami getaran harmonis. Pada keadaan tersebut amplitudo adalah dari posisi awal pegas sampai keadaan simpangan kedua. Ketika bergetar, beda akan memiliki frekeunsi dan periode getar. Persamaan keduanya dapat dituliskan sebagai berikut (tidak diturunkan mengingat ada persamaan diferensial):

Perlu ditekankan kembali bahwa faktor yang mempengaruhi frekeunsi dan periode pegas adalah konstanta pegas dan massa beban yang disimpan dalam pegas. Perhatikan pula, ketika sistem pegas lebih dari satu, konstanta pegas di atas adalah gabungannya, baik secara seri dan secara paralel.

Dua persamaan terkahir di atas adalah cara mengganti gabungan konstanta pegas untuk sistem pemasangan seri dan paralel. Keduanya sering kali bermanfaat dalam menghitung frekeunsi dan periode getaran sistem pegas.

Kaji-1: (UMPTN-1999) Seorang pelajar yang bermassa 50 kg bergantung pada ujung sebuah pegas sehingga bertambah panjang 10 cm. Dengan demikian, tetntukanlah nilai tetapan pegas yang digunakan tersebut!

Jawab:
Besaran yang diketahui.

Konstanta pegas dapat dihitung dengan kesetimbangan gaya

Latih-1: Seorang pelajar yang bermassa 60 kg bergantung pada ujung sebuah pegas yang memiliki konstanta pegas 600N/m. Dengan demikian, tetntukanlah nilai pertambahan panjang pegas ketika digantungi oleh siswa tersebut!

Kaji-2: (UM UGM 2003) Usaha yang diperlukan untuk menarik sebuah pegas sejauh 2 cm adalah 0.5 Joule. Untuk menarik pegas tersebut sejauh 4 cm, tentukanlah gaya yang perlu diberikan pada pegas tersebut!

Jawab:
Besaran yang diketahui.


Konstanta pegas dapat dihitung menggunakan persamaan perubahan energi potensial atau usaha.

Gaya pegas yang diberikan saat pertambahan panjang 4 cm adalah


Latih-2: Usaha yang diperlukan untuk menarik sebuah pegas sejauh 4 cm adalah 2 Joule. Untuk menarik pegas tersebut sejauh 8 cm, tentukanlah gaya yang perlu diberikan pada pegas tersebut!

Kaji-3: (SIPENMARU 1988) Sebuah pegas yang panjangnya 20 cm digantungkan vertikal. Kemudian ujung bawahnya diberi beban 200 gram sehingga panjangnya bertambah 10 cm. Beban ditarik 5 cm ke bawah kemudian dilepaskan sehingga begerak harmonis. Jika percepatan gravitasi 10 m/s/s, tentukanlah frekeunsi getaran sistem tersebut!

Jawab:
Besaran yang diketahui.


Konstanta pegas sistem adalah


Frekuensi getaran pegas adalah


Latih-3: (SIPENMARU 1988) Sebuah pegas yang panjangnya 30 cm digantungkan vertikal. Kemudian ujung bawahnya diberi beban 100 gram sehingga panjangnya bertambah 10 cm. Beban ditarik 5 cm ke bawah kemudian dilepaskan sehingga begerak harmonis. Jika percepatan gravitasi 10 m/s/s, tentukanlah periode getaran sistem tersebut!

Kaji-4:  (UMPTN 1997) Sebuah beban M dan beberapa pegas identik membentuk sistem pegas beban yang mengikuti skema rancangan (a) dan (b) seperti terlihat pada gambar.

Bila gesekan udara dibabaikan, kedua getaran sistem dapat menghasilkan getaran harmonis sederhanan dengan frekuensi tertentu. Kalau fa adalah frekeunsi untuk getaran sistem (a), tentukan besar frekeunsi getaran sistem (b) di atas (konstanta semua pegas identik k)!

Jawab:
Konstanta pegas pengganti untuk sistem (a)




Konstanta pegas pengganti sistem (b) adalah


Frekuensi getaran sistem (b) dapat dihitung dengan perbandingan terhadap frekuensi (a).


Latih-4: Sebuah bola dengan massa 20 gram digantung pada sepotong pegas. Kemudian bola ditarik ke bawah dari kedudukan setimbang lalu dilepaskan, ternyata terjadi getaran tunggal dengan frekeunsi 32 Hz. Jika bola diganti dengan bola bermassa 80 gram, tentukanlah frekeunsi yang akan terjadi pada getaran!

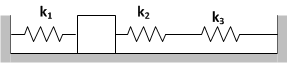
Kaji-5: (SIMAK UI 2009) Sebuah balok bermassa 144 gram di atas lantai datar licin dihubungkan dengan tiga buah pegas dengan susunan seperti pada gambar di bawah ini.

Konstanta pegas masing-masing  k1 = 20 N/m, k2 = 60 N/m, dan k3= 30 N/m. Jika balok disimpangkan dari titik setimbangnya dengan simpangan kecil, tentukanlah periode getaran harmonis yang dihasilkan!

Jawab:
Besaran yang diketahui.


Pegas k2 dan k3 dirangkain seri, sehingga kalau diganti oleh satu pegas jadi


Pegas k1 dan pengganti k2 dan k3 terangkai paralel, sehingga konstanta pegas gabungan adalah


Periode getaran sistem pegas adalah sebagai berikut:


Latih-5: (SPMB 2009) Konstanta pegas dari suatu pistol mainan anak-anak adalah 100 N/m. Sebelum ditembakkan dengan arah vertikal ke atas , peluru 10 gram menekan pegas 20 cm, tentukanlah ketinggian maksimum yang dicapai peluru setelah ditembakkkan!